Nadpłynność helu

prof. Wojciech Kempiński

Nadpłynność, czasami nazywana nadciekłością, jest zjawiskiem z obszaru fizyki kwantowej, a więc z obszaru, w którym intuicja nie zawsze podpowiada poprawne rozwiązania. Zjawisko to zostało odkryte u początków fizyki kwantowej więc pierwsze próby jego wyjaśnienia z konieczności oparte były o podstawy fizyki klasycznej. Pierwsze badania helu ciekłego możliwe były oczywiście po jego skropleniu, a to zawdzięczamy Heike Kamerligh-Onnesowi – rok 1908. Za datę powstania fizyki kwantowej uznaje się natomiast dzień 14 grudnia 1900 roku gdy na posiedzeniu Niemieckiego Towarzystwa Fizycznego w Berlinie Max Planck przedstawił wyprowadzenie prawa promieniowania ciała doskonale czarnego [1].

Spotkanie z nadpłynnością warto rozpocząć od umieszczenia wyobraźni w odpowiednim dla naszych celów obszarze podstawowych wielkości termodynamicznych jakimi są temperatura T i ciśnienie p. W tym celu warto, aby na bazie diagramu fazowego dla naturalnie występującego, w stosunkowo dużych ilościach na Ziemi, izotopu helu 4He, przypomnieć sobie, że obniżając temperaturę ciekłego helu przy ustalonym ciśnieniu, mniejszym niż 25 atm, nie uda nam się uzyskać zestalenia tej cieczy. Pierwsze sygnały związane z możliwością wystąpienia podczas obniżania temperatury w 4He “jakiejś” przemiany fazowej tam, gdzie zwykle mamy do czynienia z zestaleniem, pochodzą z badań zachowania się przenikalności elektrycznej w funkcji temperatury, przeprowadzonych w latach dwudziestych poprzedniego wieku przez W.H. Keesoma i M. Wolfkego. W Zakładzie Fizyki Niskich Temperatur Instytutu Fizyki Molekularnej Polskiej Akademii Nauk (ZFNT IFM PAN), gdzie obecnie prowadzi się liczne badania niskotemperaturowe, wykonano również pomiary zależności przenikalności elektrycznej 4He w funkcji temperatury i ciśnienia, co umożliwiło odtworzenie diagramu fazowego w obszarze, o którym będzie mowa w tym artykule. Przykładowe zachowanie się rzeczywistej składowej przenikalności elektrycznej w funkcji ciśnienia [2] i temperatury [3] 4He przedstawiają rysunki 1 i 2. Pomocnym w tworzeniu diagramu fazowego okazał się również pomiar gęstości helu przeprowadzony także w ZFNT IFM PAN – rysunek 3 [4-7]. Diagram fazowy w skali półlogarytmicznej przedstawia rysunek 4 [2]. Widoczny na tym rysunku obszar oznaczony ‘He II’ to właśnie obszar nadpłynnego helu.

a)

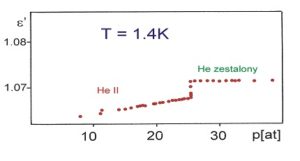
b)

Rys. 1 Zależność rzeczywistej składowej przenikalności elektrycznej 4He dla dwóch różnych temperatur poniżej punktu l
(a – 1.4 K, b – 1.7 K) w funkcji ciśnienia.

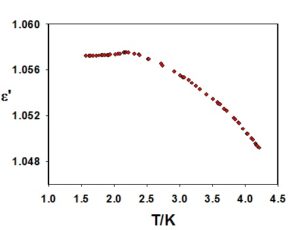
Rys. 2 Zależność rzeczywistej składowej przenikalności elektrycznej 4He w okolicy punktu l w funkcji temperatury.

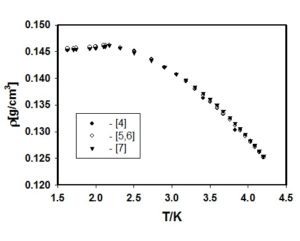
Rys. 3 Zależność gęstości 4He w okolicy punktu l w funkcji temperatury.

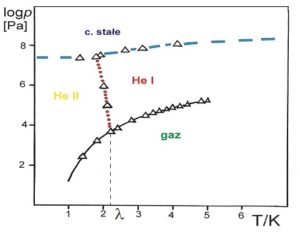
Rys. 4 Diagram fazowy 4He w skali półlogarytmicznej skonstruowany w oparciu o wyniki pomiarów, których przykładowe rezultaty zostały przedstawione na rysunkach 1-3.

Pojawienie się fazy stałej w 4He dopiero po przyłożeniu ciśnienia (około 25 atm – porównaj rysunki 1 i 2) wynika z dużej amplitudy drgań zerowych atomów helu. Pod normalnym ciśnieniem przewyższa ona odległości między atomami 4He – objętość zajmowana przez jeden atom 4He jest stosunkowo duża, rzędu 46 Å3 [8]. Wraz ze wzrostem ciśnienia amplituda drgań zerowych ulega zmniejszeniu szybciej, niż odległości pomiędzy atomami co w konsekwencji prowadzi do przejścia ciecz-ciało stałe.

Interesujące eksperymenty z zestalonym helem prowadzane są nadal. Dwa z nich warte są specjalnej wzmianki: zestalenie helu przy użyciu energii fali akustycznej [9] oraz eksperyment, w którym pokazano efekt zwany “supersolidity” [10,11]. Oba wymienione eksperymenty bezpośrednio nawiązują do głównego tematu tego rozdziału – nadpłynności. Pierwszy z nich pokazuje, jak dużą i decydującą rolę w tworzeniu kryształów helu odgrywa obszar temperaturowy, w którym one powstają – np. wybór temperatury poniżej temperatury l (por. rys 5), a więc w obszarze nadpłynności, pozwala zaobserwować rekordową prędkość wzrostu kryształów – dla kryształów o wielkości 15 mm zaobserwowano czas wzrostu 150 ns, co daje prędkość dochodzącą do 150 m/s. Możliwość tak szybkiego wzrostu kryształów związana jest z ekstremalnie wysokim przewodnictwem cieplnym nadpłynnego helu. Środowisko takie zapewnia wyjątkowo skuteczne odprowadzanie ciepła krystalizacji. Wysoka wartość przewodnictwa cieplnego nadpłynnego helu to klucz do zrozumienia eksperymentu demonstrującego samo przejście l zilustrowane na rysunku 5. Drugi z wymienionych eksperymentów do nadpłynności silnie próbuje nawiązać nazwą – termin “supersolidity” nie ma jeszcze odpowiednika polskiego, a jego dosłowne tłumaczenie “nadstałość”, chociaż nie do końca oddaje sens terminu angielskiego, to jednak podpowiada nam, że obserwowany efekt ma dużo wspólnego ze zmianą parametru, który w ciele stałym byłby odpowiednikiem lepkości cieczy. I tak rzeczywiście jest, chociaż zaobserwowana zmiana modułu sprężystości wynika raczej z obecności defektów, np. domieszki innego izotopu helu – 3He, niż ze zmian zachodzących w samym 4He [12].

Skoro nie można w procesie obniżania temperatury pod normalnym ciśnieniem uzyskać zestalenia helu, to warto zapytać, co właściwie dzieje się w podczas ochładzania ciekłego helu. Proces ten można łatwo zrealizować obniżając ciśnienie nad powierzchnią ciekłego helu – usuwamy w ten sposób wysokoenergetyczne atomy, co oznacza, że energia, a więc i temperatura układu ulega obniżeniu. Na rysunku 4 proces ten reprezentowany jest krzywą rozgraniczającą obszary ‘gaz’ – ‘He I’ (He I to ciecz zachowująca się klasycznie). Rozpoczynając proces obniżania ciśnienia par nad powierzchnią cieczy, zaobserwujemy gwałtowne wrzenie występujące w całej jej objętości (Rys. 5a). Wędrując po krzywej ‘gaz’ – ‘He I’ wraz z temperaturą w dół natrafiamy na specyficzny punkt, na rysunku 4 oznaczony literą l – przypada on w temperaturze Tl = 2.17K. W punkcie tym wrzenie objętościowe w helu zanika (Rys. 5b) a jego powierzchnia, mimo dalszego spadku ciśnienia, a więc i temperatury, pozostaje spokojna (Rys. 5c) – odparowanie zachodzi jedynie z powierzchni helu.

Rys. 5 4He w okolicy przemiany l: a/ T > Tl, b/ T ~ Tl, c/ T < Tl.
Zdjęcia wykonano w ZFNT IFM PAN

Brak objętościowego wrzenia, tzn. brak pęcherzyków pary wewnątrz cieczy poniżej punktu l, powstających w wyniku lokalnego przegrzania, świadczy o tym, że takiego przegrzania w obszarze He II wytworzyć nie można. Oznacza to, że w tym obszarze nie można wytworzyć stałej różnicy temperatur. To z kolei prowadzi wprost do wniosku, że istnieje olbrzymia różnica w przewodnictwie cieplnym (kilka rzędów wielkości) dla obszarów powyżej punktu l (He I) i poniżej tego punktu (He II). W obszarze He I ciecz zachowuje się klasycznie, a w obszarze He II hel wykazuje własności kwantowe. Nazwa obserwowanej przemiany pochodzi od kształtu zależności ciepła właściwego w funkcji temperatury przypominającego grecką literę l. Eksperyment ten na początku lat 30-tych poprzedniego wieku przeprowadzony został przez W.H. Keesoma w Lejdzie – Rys. 6. Termin nadpłynność (nadciekłość) pojawił się po serii eksperymentów przeprowadzonych w latach 30-tych poprzedniego wieku przez P.L. Kapicę [13,14] i J.F. Allena i A.D. Missenera [15,16] z ciekłym helem, który np. poniżej temperatury l pokonywał bez przeszkód (bez tarcia) szczeliny (kapilary) o średnicach rzędu 10-5 cm.

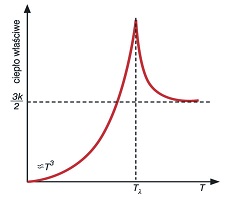
Rys. 6 Zależność ciepła właściwego w funkcji temperatury w okolicy punktu l.

Pierwszą próbą wyjaśnienia zachowania się helu w obszarze H II był tzw. model dwupłynowy. Model ten opiera się o podstawowe założenia, z których pierwsze mówi, że hel poniżej punktu l można opisać – zakładając pojawienie się rozdziału na dwie składowe – składową normalną, która posiada wszystkie własności cieczy występującej powyżej punktu l i dodatkową składową, składową nadpłynną, która pojawia się po przejściu fazowym do obszaru He II. Wówczas całkowita gęstość układu jest sumą dwóch wyżej wymienionych składowych. Drugie z założeń mówi, że składowa nadpłynna pozbawiona jest lepkości oraz entropii i posiada bardzo niską energię. Składowa ta odgrywa rolę tła, na którym manifestują się różnego rodzaju wzbudzenia charakterystyczne dla cieczy klasycznej. Obie składowe można próbować rozdzielić przy pomocy tzw. filtra entropowego. Jest on barierą dla cieczy zachowującej się klasycznie, a nie stanowią żadnej przeszkody dla składowej nadpłynnej (pozbawionej lepkości). Trzecie, ostatnie założenie modelu dwupłynowego mówi, że wzajemny stosunek dwóch składowych gęstości jest funkcją temperatury. Niska energia składowej nadpłynnej kojarzona jest z kwantowym stanem zwanym kondensatem Bosego-Einsteina. Przemiana l nazywana jest więc często kondensacją Bosego-Einsteina [17] a składowa nadpłynna cieczą kwantową. Kondensacja ta polega na obsadzaniu najniższych poziomów energetycznych przez atomy lub cząstki będące bozonami (charakteryzowanymi całkowitą liczbą spinową). Takimi cząstkami są właśnie atomy helu. W odróżnieniu od fermionów, bozony, których nie obowiązuje zasada Pauliego, zdolne są do obsady tych samych poziomów energetycznych. W związku z tym kondensacja Bosego-Einsteina to kondensacja cząstek na najniższym poziomie energetycznym zachodząca w nierzeczywistej przestrzeni pędów. Model dwupłynowy jako podejście fenomenologiczne stał się podstawą teorii Landaua, w której podstawowymi wzbudzeniami pojawiającymi się na tle fazy nadpłynnej są fonony i rotony. R. Feynman w swoim opisie zjawiska nadpłynności rotony określił jako “duchy” wirów tworzących się w fazie nadciekłej, gdy naczynie z tą cieczą przekroczy obrotową prędkość krytyczną. Teorie Landaua [18] i Feynmana [19] oparte są o widmo energetyczne helu, w którym wyróżnia się dwie gałęzie: fononową i rotonową.

Model dwupłynowy znalazł silne potwierdzenie w słynnym doświadczeniu Andronkaszwiliego [20], którego współczesna wersja [21] odpowiada na ważne pytanie – ile atomów helu niezbędnych jest do utworzenia fazy nadpłynnej. Odpowiedź udzielona w pracy [21] brzmi – 60! Model dwupłynowy doskonale tłumaczy również takie efekty jak fontannowy czy pająk Kapicy. Efekty te należą do grupy zjawisk zwanych termomechanicznymi, a więc generowanymi ciepłem dostarczanym do nadpłynnego helu. Oprócz tych efektów obserwuje się również efekt mechanokaloryczny, w którym zmiany mechaniczne (np. pokonanie filtra entropowego) prowadzą do zmian temperatury. Oba te zjawiska ujęte zostały równaniem Londona:

(1) 

gdzie współczynniki łączące różnice temperatur i ciśnień to r – gęstość (całkowita – helu nadpłynnego i normalnego) oraz S – entropia.
Z równania (1) wynika, że pojawienie się lokalnych gradientów temperatury prowadzi do wygenerowania różnicy ciśnień i na odwrót – wygenerowanie w układzie różnicy ciśnień prowadzi do pojawienia się różnicy temperatur. Drugi z efektów tłumaczy możliwość zaobserwowania w nadpłynnym helu tzw. drugiego dźwięku, który mierzony jest przy pomocy termometru. Wynika to z trzeciego założenia modelu dwupłynowego – fala drugiego dźwięku to wynik przesunięcia fazowego drgających niezależnie składowych normalnej i nadpłynnej – fala temperatury pojawia się wówczas w wyniku wystąpienia lokalnych zmian gęstości, których wzajemny stosunek jest funkcją temperatury. Oprócz drugiego dźwięku w helu nadpłynnym możliwe jest zaobserwowanie dźwięków trzeciego i czwartego – obserwuje się je w błonach helowych pokrywających ścianki naczynia, w którym hel jest przechowywany. W skrajnych przypadkach efekt ten może doprowadzić do opróżnienia takiego naczynia w wyniku tzw. przepływu potencjalnego [8].

Przypisy:
[1] M. Planck, Annalen der Physik, 4 (1991) 553
[2] T. Żuk, W. Kempiński, Z. Trybuła, J. Pichet, przygotowane do druku
[3] J. Stankowski, S. Sitarz, Z. Trybuła, W. Kempiński, T. Żuk, Acta Phys. Polon. A70 (1986) 291
[4] W. Kempiński, T. Żuk, J. Stankowski, S. Sitarz, Fiz. Niz. Tiemp. 14(5) (1988) 451
[5] E.C. Kerr, R.D. Taylor, Ann. Phys. 26 (1964) 292
[6] E.C. Kerr, J. Chem. Phys. 26 (1957) 13
[7] B.N. Eselson, W.G. Iwantsow, P.S. Nowikow, R.I. Shcherbachenko, U.F.Z. 14 (1969) 1837
[8] C.T. Lane “Nadpłynność” PWN, Warszawa, 1967
[9] X. Chavanne, S. Balibar, F. Caupin, Phys. Rev. Lett. 86 (2001) 5506
[10] E. Kim, M.H.W. Chan, Nature 427 (2004) 225
[11] E. Kim, M.H.W. Chan, Science 305 (2004) 1941
[12] J. Day, J. Beamish, Nature 450 (2007) 853
[13] P.L. Kapica, Proc. Roy. Soc. A 147 (1934) 189
[14] P.L. Kapica, Dok. Akad. Nauk SSSR 18 (1938) 21
[15] J.F. Allen, A.D. Missener, Nature 141 (1938) 75
[16] J.F. Allen, H. Jones, Nature 141 (1938) 243
[17] A.I. Anselm, Podstawy fizyki statystycznej i termodynamiki, PWN, Warszawa 1978
[18] L. Landau, J. Phys. (USSR) 5(1941) 71
[19] R.P. Feynman, Wykłady z mechaniki statystycznej, PWN, Warszawa 1980
[20] E.L. Andronikashvili, J. Exp. Theoret. Phys. (USSR) 18 (1948) 424
[21] S. Grebenev, J.P. Toennies, A.F. Vilesov, Science 279 (1998) 2083

(Artykuł opublikowany w poradniku wydanym z okazji “100-lecia skroplenia helu przez Heike Kameringha-Onnesa”, 10 lipca 2008 Odolanów)